1.4 Sistemes d'equacions lineals. Els sistemes d'equacions lineals expressen dependències lineals entre variables (incògnites). Resoldre el sistema és trobar valors d'aquestes variables que satisfan tots els lligams simultàniament. Si els lligams són massa restrictius (resp. massa laxes), uns tals valors poden no existir (resp. no estar completament determinats).

Alguns exemples senzills.
Problema 9   Determineu dos valors numèrics tals que el primer més el doble del segon sumin 6.
Solució   Representem les quantitats desconegudes per dues lletres x i y, que s'anomenen variables o incògnites, i imposem la condició x + 2y = 6 . A simple vista es veu que hi ha molts possibles valors de x i y que satisfan la igualtat (equació) anterior, p. ex. x=2 i y=2, o també x=0 i y=3, etc. El problema no està determinat.

Problema 10   Determineu dos valors numèrics tals que un qualsevol d'ells més el doble de l'altre sumin 6.
Solució   En aquest cas hem d'imposar dues condicions, x + 2y = 6 però també y + 2x = 6 .Tenim per tant dues equacions i dues incògnites. El problema està determinat, i la única solució és ara x = y = 2 .

Problema 11   Determineu dos valors numèrics tals que un qualsevol d'ells més el doble de l'altre sumin 6, i que el seu producte valgui 8.
Solució   En aquest cas hem d'imposar tres condicions, x + 2y = 6 , y + 2x = 6 i encara xy = 8 . Hi ha tres equacions i dues incògnites. El problema no té solució (sistema incompatible), o sigui, no existeixen uns tals valors numèrics x i y que satisfacin les tres condicions demanades.

A més, en aquest cas el sistema NO és lineal, perquè la tercera equació conté un producte entre dues variables.

Sistemes d'equacions lineals. Expressió matricial.
Un sistema d'equacions és un conjunt d'equacions que s'han de satisfer simultàniament.
Si aquestes equacions contenen només sumes de valors numèrics (escalars) multiplicats per variables (incògnites) i valors numèrics independents, diem que el sistema és lineal.

Tot sistema lineal d'equacions es pot escriure com a producte de matrius Ax = b on:
   
    • A és la matriu de coeficients
    • x és el vector d'incògnites
    • b és el terme independent
Com que el vector d'incògnites x no aporta cap informació, sovint s'utilitza una expressió matricial compacta (A | b) en comptes del producte Ax = b.

exemple 12   En el cas dels tres problemes de l'apartat anterior, es té:
equacions
producte de matrius
expressió matricial
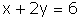
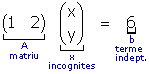
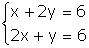
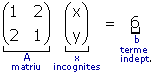
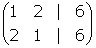
No és lineal.
No admet expressió com a producte de matrius. 		No n'admet.

Resolució de sistemes lineals. El mètode de Gauss. Consisteix en fer zeros a sota de la diagonal principal de la matriu.
exercici 5   problema 1.8

Discussió de sistemes. No cal aplicar el mètode de Gauss (o qualsevol altre) per a saber si un sistema té o no solució, o si aquesta solució serà única.

Teorema de Rouché-Frobënius
El sistema Ax=b és compatible (o sigui, té solució) si i només si rang(A)=rang(A,b).

A més, la solució depèn de m=n-rang(A) paràmetres, on n representa el nombre d'incògnites.

exercici 6   problema 1.11

¿