3.3 Canvi d'eixos (o de base).
A continuació s'estudiarà com varien les coordenades d'un punt en funció dels eixos
de referència escollits, quan l'origen es manté fix .
Les direccions i unitats de mesura dels eixos venen determinats únicament
pels vectors de la base. D'aquí que es parli indistintament de
canvi d'eixos o de canvi de base .
Canvi d'eixos (o de base).
Comencem amb un exemple.
Problema. Es considera les referències
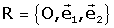 i i
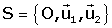 on on
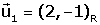 i
i 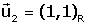 . .
Si P té coordenades 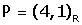 en referència R, quines són les seves coordenades
en referència R, quines són les seves coordenades
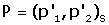 en referència S?
en referència S?
|
|
Solució gràfica. Si Q i P són les
projeccions de P sobre els nous eixos de coordenades, llavors
p'1 és la longitud del segment 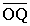
p'2 és la longitud del segment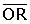 . .
|
Solució algèbrica. Es considera la matriu M que té per
columnes les coordenades dels vectors 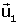
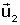 en referència R, i es
calcula la seva inversa M-1. en referència R, i es
calcula la seva inversa M-1.
|
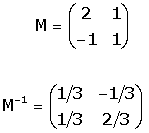
|
Les coordenades de P en referència S s'obtenen efectuant el
producte de M-1 per les coordenades
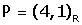
|
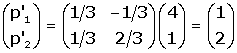
|
En general, si 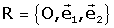 i
i
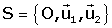 són dues referències al pla i es coneixen les
coordenades en referència R del vectors de S,
són dues referències al pla i es coneixen les
coordenades en referència R del vectors de S, 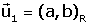 i
i 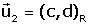 llavors la matriu
llavors la matriu 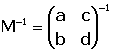 s'anomena matriu del canvi de base (o d'eixos) de R a S, i satisfà
s'anomena matriu del canvi de base (o d'eixos) de R a S, i satisfà
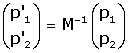 per a qualsevol punt
per a qualsevol punt
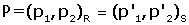 .
.
- La matriu M-1 és la única que satisfà la propietat anterior.
- El procés descrit és del tot general, i serveix també per a referències amb 3 o més
vectors (espai, ...)
exercici: problema 3.6 a,b i c.
Justificació de l'ús de la matriu inversa.
(segueix exemple anterior) Tenint en compte que les coordenades
de P en referència S són els coeficients p'1,
p'2 utilitzats en la combinació lineal
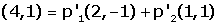 Per tant, p'1, p'2 són les solucions del sistema
Per tant, p'1, p'2 són les solucions del sistema
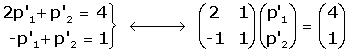 que no són altres que
que no són altres que
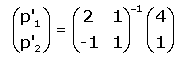
|
En general, la combinació lineal a considerar és 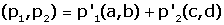 que matricialment s'escriu com
que matricialment s'escriu com
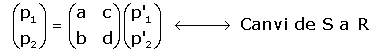
o, alternativament
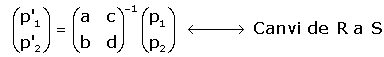
El canvi invers d'eixos o de base (canvi de S a R).
Normalment, el que coneixem són les coordenades
d'un punt P en la referència R original del
problema,  ,
i el que volem saber són les coordenades de P
en una referència "nova", S, introduïda
posteriorment.
,
i el que volem saber són les coordenades de P
en una referència "nova", S, introduïda
posteriorment.
Però també es pot plantejar el problema invers:
conegudes les coordenades de P en la referència
S, 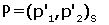 , determinar
les coordenades de P en la referència R,
, determinar
les coordenades de P en la referència R,
 .
.
Observeu (final apartat anterior) que la matriu M resol el problema plantejat.
M és la matriu del canvi de S a R.
¿
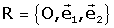 i
i
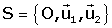 on
on
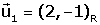 i
i 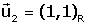 .
.
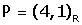 en referència R, quines són les seves coordenades
en referència R, quines són les seves coordenades
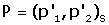 en referència S?
en referència S?
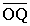
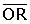 .
.
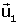
 en referència R, i es
calcula la seva inversa M-1.
en referència R, i es
calcula la seva inversa M-1.
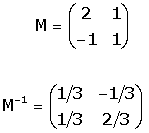
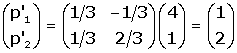
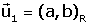 i
i 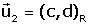 llavors la matriu
llavors la matriu 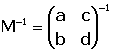 s'anomena matriu del canvi de base (o d'eixos) de R a S, i satisfà
s'anomena matriu del canvi de base (o d'eixos) de R a S, i satisfà
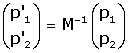 per a qualsevol punt
per a qualsevol punt
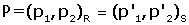 .
.
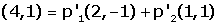
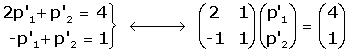
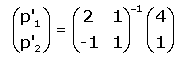
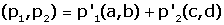 que matricialment s'escriu com
que matricialment s'escriu com
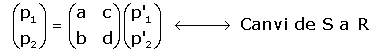
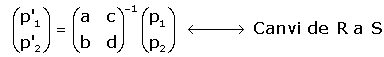
 ,
i el que volem saber són les coordenades de P
en una referència "nova", S, introduïda
posteriorment.
,
i el que volem saber són les coordenades de P
en una referència "nova", S, introduïda
posteriorment.
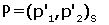 , determinar
les coordenades de P en la referència R,
, determinar
les coordenades de P en la referència R,