1.2 Determinants. El determinant d'una matriu quadrada ens informa, d'una banda, de la dependència lineal entre els seus vectors fila (o columna).
D'altra banda permet calcular el volum del sòlid que té aquells vectors com a arestes.
També dóna informació sobre la orientació de la base.
Càlcul del determinant. El determinant d'una matriu quadrada es defineix com la suma de tots els productes (amb signe) on hi intervenen un únic element per cada fila i un únic per cada columna.

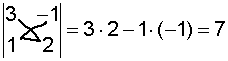
Exemple 4 determinant 2x2.
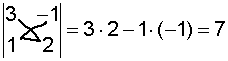
Exemple 5 determinant 3x3 (estrella).
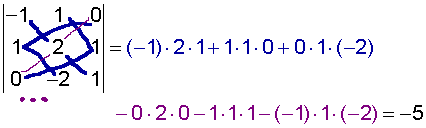
Exemple 6 determinant nxn (desenvolupant per files o columnes).
El mètode de Gauss per a la resolució de sistemes d'equacions es pot utilitzar també (amb precaució) per a calcular determinants.

Interpretació geomètrica. El determinant de dos vectors mesura l'àrea del paral.lelògram que els té per costats. per què?

El determinant de tres vectors és el volum del paral.lelepíped que determinen.

Com a conseqüència, el determinant de dos vectors paral.lels o de tres vectors coplanaris és nul.

En general, el determinant de n vectors linealment dependents és nul.

exercici 3 problema 1.5

¿