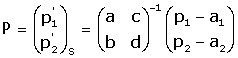Lliçó 3 Sistemes de referčncia.
Descripció.
S'introdueix la noció de sistema de referčncia, i s'estudia com varien les coordenades
d'un punt quan s'expressa en referčncies diferents.
3.1 El problema del canvi de referčncia.
Sistemes de referčncia.
Una referčncia R a la recta, pla, espai ... consta
d'un punt O i d'una base
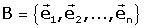 de l'espai vectorial associat.
de l'espai vectorial associat.
El punt O representa l'origen de coordenades, mentre que els vectors de la base
determinen les direccions dels eixos de projecció.
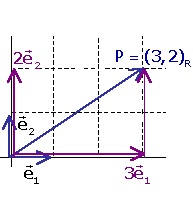
L'exemple més habitual és la referčncia cartessiana al pla (o a l'espai):
Observeu l'equivalčncia entre:
1.- projectar el punt P sobre els eixos i mesurar-ne les projeccions, i
2.- obtenir el vector OP com a combinació lineal dels de la base.
En general, 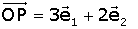 si P=(p1, p2), o bé
si P=(p1, p2), o bé
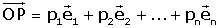 si treballem a Rn.
si treballem a Rn.
Les coordenades d'un vector són les del seu punt extrem quan el vector estŕ ancorat a l'origen.
Noteu que l'origen de coordenades no influeix en les coordenades d'un vector, i que aquestes
depenen només de la base.
Es parla de les coordenades d'un vector respecte d'una base B,
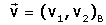 i no respecte d'una referčncia R.
i no respecte d'una referčncia R.
Hi ha d'altres tipus de coordenades que no
esdudiarem aquest curs, perň sí més endavant
(Per exemple, les coordenades polars
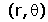 )
)
Canvi de referčncia.
Sistemes de referčncia diferents assignen coordenades diferents a un mateix punt del pla (espai, ...).
|
|
Problema.
Si 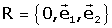 i i
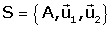 són
dues referčncies del pla, i el punt P té coordenades són
dues referčncies del pla, i el punt P té coordenades 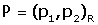 en la primera referčncia, quines són les coordenades de P
en la segona referčncia
en la primera referčncia, quines són les coordenades de P
en la segona referčncia
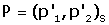 ? ?
|
Un canvi de referčncia es pot desglossar en dues operacions diferents: canvi d'origen i canvi d'eixos.
3.2 Canvi d'origen.
Comencem amb un exemple.
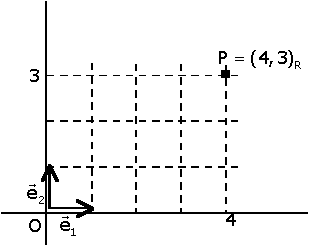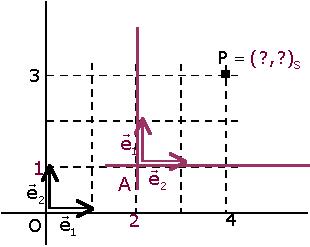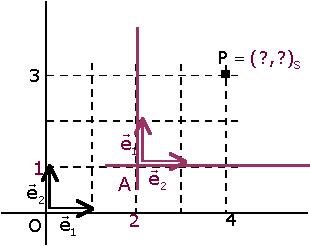
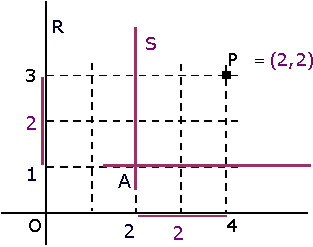
Problema. Sigui  una referčncia al pla (la referčncia inicial o canňnica), i P un punt de coordenades (3,3)R.
una referčncia al pla (la referčncia inicial o canňnica), i P un punt de coordenades (3,3)R.
Introduďm una nova referčncia 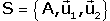 (eixos iguals, origen diferent) amb A=(2,1)R.
(eixos iguals, origen diferent) amb A=(2,1)R.
Quines són les coordenades de P en referčncia S?
|
|
|
Solució.
S'observa que les projeccions de P sobre els nous eixos s'obtenen
restant les projeccions de P i A sobre els eixos de la referčncia inicial.
Per tant,
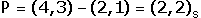
|
|
|
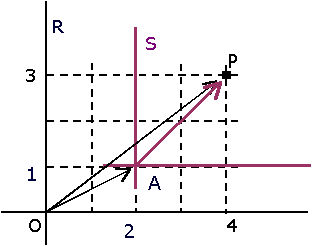
Alternativament, podem observar que
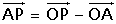
que escrit en coordenades respecte a la base
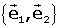 resulta resulta
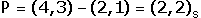
|
En general, per a un punt P del pla, (espai,...) i dues referčncies 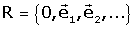 i
i
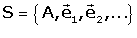 es satisfŕ:
es satisfŕ:
(p'1,p'2,...) = (p1,p2,...) - (a1,a2,...)
on (p1,p2,...) són les coordenades de P en la referčncia inicial R
(p'1,p'2,...) són les coordenades de P en la nova referčncia S, i
(a1,a2,...) són les coordenades del nou origen A en la referčncia inicial R.
3.3 Canvi d'eixos (o de base).
A continuació s'estudiarŕ com varien les coordenades d'un punt en funció dels eixos
de referčncia escollits, quan l'origen es manté fix .
Les direccions i unitats de mesura dels eixos venen determinats únicament
pels vectors de la base. D'aquí que es parli indistintament de
canvi d'eixos o de canvi de base .
Canvi d'eixos (o de base).
Comencem amb un exemple.
Problema. Es considera les referčncies
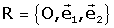 i i
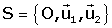 on on
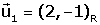 i
i 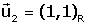 . .
Si P té coordenades 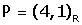 en referčncia R, quines són les seves coordenades
en referčncia R, quines són les seves coordenades
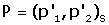 en referčncia S?
en referčncia S?
|
|
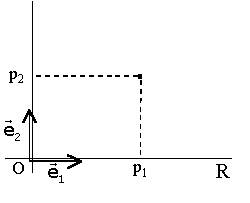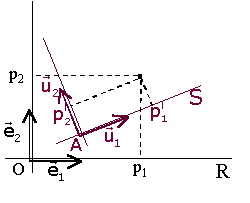
Solució grŕfica. Si Q i P són les
projeccions de P sobre els nous eixos de coordenades, llavors
p'1 és la longitud del segment 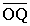
p'2 és la longitud del segment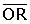 . .
|
Solució algčbrica. Es considera la matriu M que té per
columnes les coordenades dels vectors 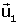
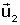 en referčncia R, i es
calcula la seva inversa M-1. en referčncia R, i es
calcula la seva inversa M-1.
|
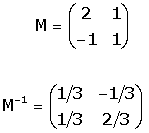
|
Les coordenades de P en referčncia S s'obtenen efectuant el
producte de M-1 per les coordenades
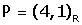
|
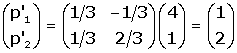
|
En general, si 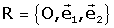 i
i
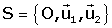 són dues referčncies al pla i es coneixen les
coordenades en referčncia R del vectors de S,
són dues referčncies al pla i es coneixen les
coordenades en referčncia R del vectors de S, 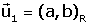 i
i 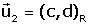 llavors la matriu
llavors la matriu 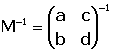 s'anomena matriu del canvi de base (o d'eixos) de R a S, i satisfŕ
s'anomena matriu del canvi de base (o d'eixos) de R a S, i satisfŕ
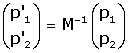 per a qualsevol punt
per a qualsevol punt
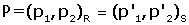 .
.
- La matriu M-1 és la única que satisfŕ la propietat anterior.
- El procés descrit és del tot general, i serveix també per a referčncies amb 3 o més
vectors (espai, ...)
exercici: problema 3.6 a,b i c.
Justificació de l'ús de la matriu inversa.
(segueix exemple anterior) Tenint en compte que les coordenades
de P en referčncia S són els coeficients p'1,
p'2 utilitzats en la combinació lineal
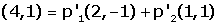 Per tant, p'1, p'2 són les solucions del sistema
Per tant, p'1, p'2 són les solucions del sistema
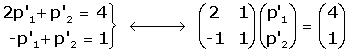 que no són altres que
que no són altres que
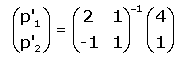
|
En general, la combinació lineal a considerar és 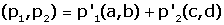 que matricialment s'escriu com
que matricialment s'escriu com
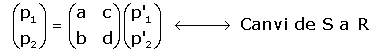
o, alternativament
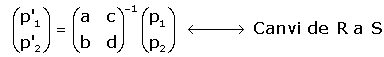
El canvi invers d'eixos o de base (canvi de S a R).
Normalment, el que coneixem són les coordenades
d'un punt P en la referčncia R original del
problema,  ,
i el que volem saber són les coordenades de P
en una referčncia "nova", S, introduďda
posteriorment.
,
i el que volem saber són les coordenades de P
en una referčncia "nova", S, introduďda
posteriorment.
Perň també es pot plantejar el problema invers:
conegudes les coordenades de P en la referčncia
S, 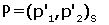 , determinar
les coordenades de P en la referčncia R,
, determinar
les coordenades de P en la referčncia R,
 .
.
Observeu (final apartat anterior) que la matriu M resol el problema plantejat.
M és la matriu del canvi de S a R.
3.4 Canvi global de referčncia.
Tractem ara la situació més general, en quč la referčncia original
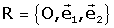 i la nova referčncia
i la nova referčncia
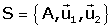 no mantenen cap element, ni
origen ni eixos, en comú.
no mantenen cap element, ni
origen ni eixos, en comú.
Aquest cas es pot reduďr a una seqüčncia de dos ja vistos:
1. Canvi d'origen (de O a A).
2. Canvi de base (de 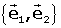 a
a
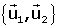 .
.
Nota: l'ordre no és rellevant.
Descomposició en dos canvis successius.
Problema. Es considera les referčncies
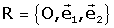 i i
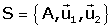 on on
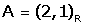 , ,
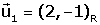 i
i 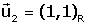 . .
Si P té coordenades 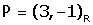 en referčncia R, quines són les seves coordenades
en referčncia R, quines són les seves coordenades
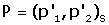 en referčncia S?
en referčncia S?
|
Solució.
Introduďm una referčncia auxiliar
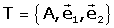 . Les coordenades de P
en referčncia T són (canvi d'origen): . Les coordenades de P
en referčncia T són (canvi d'origen): 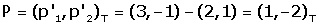
Efectuant ara un canvi d'eixos de T a S s'obté:
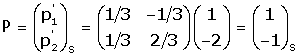
|
En general, si 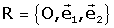 i
i
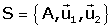 són les dues referčncies al pla i es coneixen les
coordenades en referčncia R dels vectors de S,
són les dues referčncies al pla i es coneixen les
coordenades en referčncia R dels vectors de S, 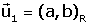 i
i 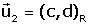 i de l'origen
i de l'origen 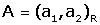 , llavors
, llavors
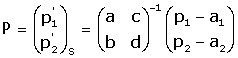
El procés descrit és del tot general, i serveix també per a referčncies amb 3 o més vectors (espai, ...)
El canvi invers (canvi de S a R).
Si es coneix les coordenades d'un punt en la nova referčncia S,
les coordenades en la referčncia original R s'obtenen fent:

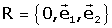 .
.
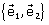 són un parell de vectors
(normalment, es prenen ortogonals i unitaris), que formen base de R2.
són un parell de vectors
(normalment, es prenen ortogonals i unitaris), que formen base de R2.
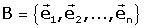 de l'espai vectorial associat.
de l'espai vectorial associat.
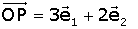
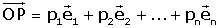 si treballem a Rn.
si treballem a Rn.
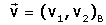 i no respecte d'una referčncia R.
i no respecte d'una referčncia R.
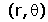 )
)

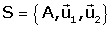 són
dues referčncies del pla, i el punt P té coordenades
són
dues referčncies del pla, i el punt P té coordenades 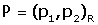 en la primera referčncia, quines són les coordenades de P
en la segona referčncia
en la primera referčncia, quines són les coordenades de P
en la segona referčncia
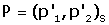 ?
?
 una referčncia al pla (la referčncia inicial o canňnica), i P un punt de coordenades (3,3)R.
una referčncia al pla (la referčncia inicial o canňnica), i P un punt de coordenades (3,3)R.
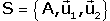 (eixos iguals, origen diferent) amb A=(2,1)R.
(eixos iguals, origen diferent) amb A=(2,1)R.

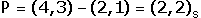


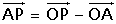
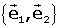 resulta
resulta
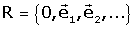 i
i
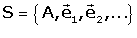 es satisfŕ:
es satisfŕ:
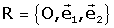 i
i
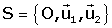 on
on
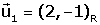 i
i 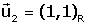 .
.
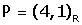 en referčncia R, quines són les seves coordenades
en referčncia R, quines són les seves coordenades
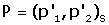 en referčncia S?
en referčncia S?
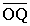
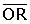 .
.
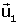
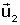 en referčncia R, i es
calcula la seva inversa M-1.
en referčncia R, i es
calcula la seva inversa M-1.
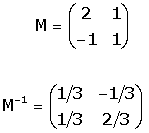
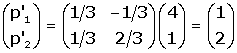
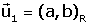 i
i 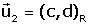 llavors la matriu
llavors la matriu 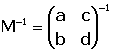 s'anomena matriu del canvi de base (o d'eixos) de R a S, i satisfŕ
s'anomena matriu del canvi de base (o d'eixos) de R a S, i satisfŕ
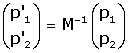 per a qualsevol punt
per a qualsevol punt
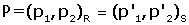 .
.
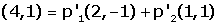
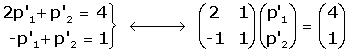
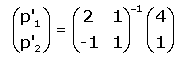
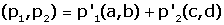 que matricialment s'escriu com
que matricialment s'escriu com
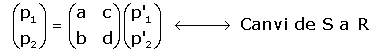
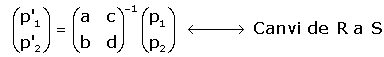
 ,
i el que volem saber són les coordenades de P
en una referčncia "nova", S, introduďda
posteriorment.
,
i el que volem saber són les coordenades de P
en una referčncia "nova", S, introduďda
posteriorment.
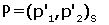 , determinar
les coordenades de P en la referčncia R,
, determinar
les coordenades de P en la referčncia R,
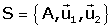 no mantenen cap element, ni
origen ni eixos, en comú.
no mantenen cap element, ni
origen ni eixos, en comú.
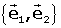 a
a
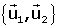 .
.
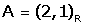 ,
,
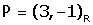 en referčncia R, quines són les seves coordenades
en referčncia R, quines són les seves coordenades
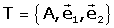 . Les coordenades de P
en referčncia T són (canvi d'origen):
. Les coordenades de P
en referčncia T són (canvi d'origen): 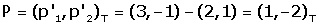
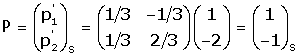
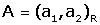 , llavors
, llavors